Es soll ermittelt werden, wie schnell sich die Massen bewegen, wenn sie unterschiedlich sind und wenn die Hebellängen verändert werden. Dabei werden die Trägheit der Massen verglichen. Hebel und Aufhängepunkte werden als masselos angesehen.
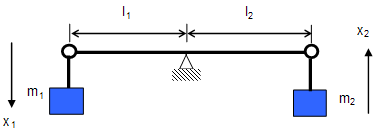
Hebel in Bewegung
Ein klassisches Beispiel für die Anwendung einer strukturierten Analyse. Hier wird die Beeinflussung der Massen auf den Bewegungsvorgang nur durch die strukturierte Analyse deutlich.
Fragestellung zur Analyse
Die Frage ist also, wie schnell bewegt sich Masse 1 nach unten und Masse 2 nach oben? Oder im Einzelnen: Was passiert, wenn die Massen ungleich sind oder bei gleichen Massen, die Hebel verändert werden?
Hilfe zur Selbsthilfe
- Lösungsansatz
- Gleichungssystem
- Blockstruktur-Hebel
- Blockstruktur-System
- Vorgaben
- Lösung durch Iteration
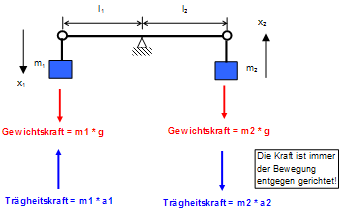
Lösungsansatz
Gesetz der Trägheit
Bei der Bewegung ist die Trägheitskraft immer der Bewegung entgegen gerichtet.
Sie will ‚in Ruhe‘ bleiben.
Erfolgt die Bewegung gegen die Erdanziehung, dann ist die Beschleunigung a = g.
Momentensatz
Helebelgesetz
Geschwindigkeit und Beschleunigung
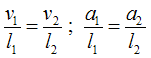
Bewegungsgesetze
Der Hebel soll sich, wenn kein Gleichgewicht herrscht, in der angegebenen Art bewegen. Diese Annahme ist erforderlich, damit die Vorzeichen in den Gleichungen festgelegt sind.
Mit dem Gesetz Kraft * Kraftarm = Last * Lastarm kann man jetzt alle Momente auf der Seite 1 und auf der Seite 2 bestimmen.
Auch hier kann man durch eine Iteration in einer Tabelle zu einer Lösung kommen.
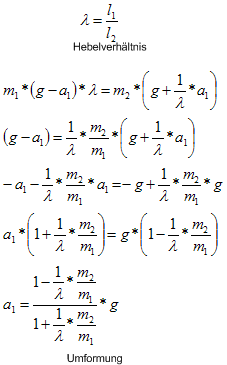
Gleichungssystem mit Umformung
Ausgehend von dem Momentensatz und dem Hebelverhältnis entsteht ein Gleichungssystem für den Augenblick. In diesen Gleichungen werden nur die Verhältnisse ausgedrückt. Die Bewegung, also die Zeit, findet keine Berücksichtigung.

Hebelgestz

Geschwindigkeitsgesetz
Basisgleichungen
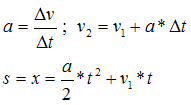
Basisgleichungen
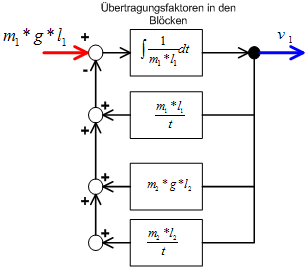
Blockstruktur des Doppelhebels
Das Gesamtsystem setzt sich aus den Teilsystemen in der Form zusammen, dass die Wirkung der Teilsysteme bildlich als Addition oder Subtraktion auf den Eingang zurück geführt wird.
Aus dieser Kombination kann dann die Gleichung für das Gesamtsystem gebildet werde, oder die Ergebnisse der Teilsysteme werden in der bildlich dargestellten Form addiert bzw. subtrahiert.
| Schrittrechnung | |||||
|---|---|---|---|---|---|
| Lösung |
